Adaptive pre-processing of Directed Acyclic Graphs

A new algorithm for reachability and least upper bound lookups

Computer component We present a unified framework for pre-processing Directed Acyclic Graphs (DAGs) to lookup reachability between two vertices as well as compute the least upper bound of two vertices in constant time.

Our framework builds on the adaptive pre-processing algorithm for constant time reachability lookups presented in [1] and we have extended the approach in [1] to lookup least upper bound of a vertex-pair in [2].

Algorithms for pre-processing DAGs do not normally exploit the structural variety in DAGs. As a first step, our approach decomposes the DAG and abstracts away from interconnections between vertices to those between sets of vertices (which we call clusters). Consequently, the pre-processing algorithm operates at a coarser granularity compared to connections between vertices.

Our approach seamlessly adapts the pre-processing overhead based on the size and incidence of clusters in the DAGs and greatly reduces the computational costs of pre-processing from super-cubic to near-linear for sparse graphs. While the proposed framework can be applied to a wide variety of fields, we present its application to the field of computer security which is the focus of our research.

Applications to security

The unified framework has a direct application to the analysis of programs for verifying confidentiality (or integrity) of information.

Consider a program shown in figure 1 where we read 4 inputs (IP1 through IP4) and produce 4 outputs (OP1 through OP4). Each of these inputs could be associated with a privilege level that defines the level of clearance required to access that information.

Similarly, when the outputs of the program are written back, they are stored with an associated privilege level. In order to ensure confidentiality is preserved for the inputs, it is necessary that the outputs must have a privilege level that is at least as restrictive as the inputs.

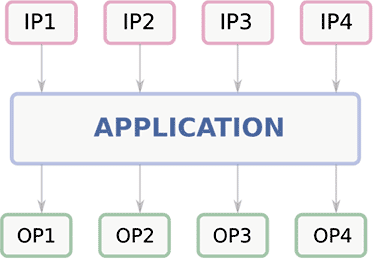
Figure 1: A program reading 4 inputs (marked IP1 through IP4) and producing 4 outputs (marked OP1 through OP4)

Figure 1: A program reading 4 inputs (marked IP1 through IP4) and producing 4 outputs (marked OP1 through OP4)

Normally, discrete privilege levels are ordered using a security lattice to define relative access levels allowed at each privilege level.

For subsequent discussions, let us assume that the privilege levels for the inputs are represented as ip1, ip2, ip3 and ip4 for IP1, IP2, IP3 and IP4 respectively and the output privilege levels are represented as op1, op2, op3 and op4 respectively.

Additionally, let us assume that these levels are ordered over a security lattice. In this context, in order to ensure confidentiality of inputs, it is necessary that glb(ip1, ip2, ip3, ip4) < lub(op1, op2, op3, op4). Here, the least upper bound or lub, greatest lower bound or glb (dual of lub) and < operations correspond to the join, meet (dual of join) and ordering lookups over the lattice that defines an ordering over the discrete privilege levels.

As an example, we now consider two different security lattices defining orderings for these security levels in figure 2 and figure 3. The lattice in figure 2 prohibits flow through the application while the one in figure 3 permits it. The rationale behind these flow decisions is explained as follows.

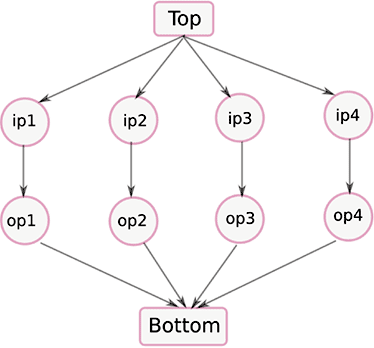
Figure 2: A security lattice with top and bottom elements that prohibits flow through the application in Figure 1 

Figure 2: A security lattice with top and bottom elements that prohibits flow through the application in Figure 1

In figure 2, the meet of ip1 through ip4 is the Bottom element and join of op1 through op4 is the Top element. This violates the constraint glb(ip1, ip2, ip3, ip4) < lub(op1, op2, op3, op4). Therefore, if we have an ordering over the security levels as described in figure 2, it would lead to a breach of confidentiality of the inputs. 

In figure 3, however, we have X as the meet of the inputs ip1 through ip4 and we have Y as the join of the outputs op1 through op4 that satisfy our constraint for preserving confidentiality of inputs.

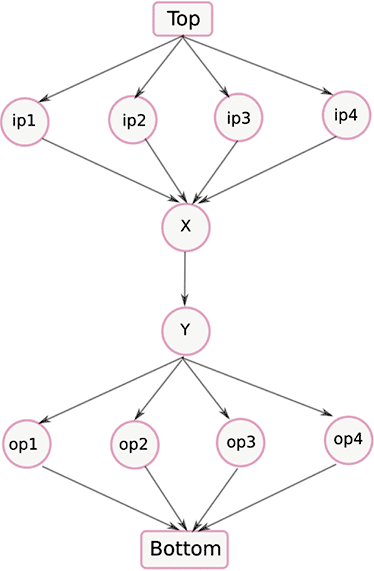
Figure 3: A security lattice with top and bottom elements that permits flow through the application in Figure 1 

Figure 3: A security lattice with top and bottom elements that permits flow through the application in Figure 1

As evidenced from the above example, our framework can be relied upon to pre-process security lattices and answer ordering/meet/join lookups in constant time.

These lookups are central to verifying confidentiality and are often the main bottleneck in analysing large pieces of software.

Additionally, real world security lattices are large and complex (more details can be found on the download page) which require efficient algorithms that support these lookups.

References

  • [1] Haixun Wang; Hao He; Jun Yang; Yu, P.S.; Yu, J.X., "Dual Labeling: Answering Graph Reachability Queries in Constant Time," in Data Engineering, 2006. ICDE '06. Proceedings of the 22nd International Conference on , vol., no., pp.75-75, 03-07 April 2006
  • [2] S. K. Dash, S.B. Scholz, B. Christianson and S. Herhut. "A scalable approach to computing Lowest Common Ancestors in Directed Acyclic Graphs", Theoretical Computer Science (TCS), Issue 513, pp. 25-37, November 2013.