Strongly-focussed Gaussian beams
Optical trapping requires the use of strongly focused laser beams. Such beams cannot be described by the commonly used paraxial model. We have proposed the following family of wave equation solutions representing beams that are not restricted to the paraxial case. In cartesian coordinates x, y, z, the set can be expressed as:
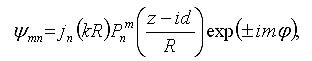
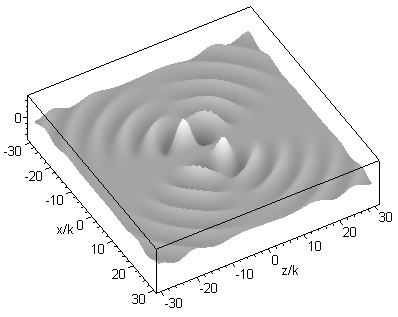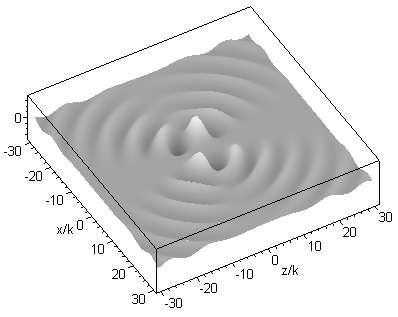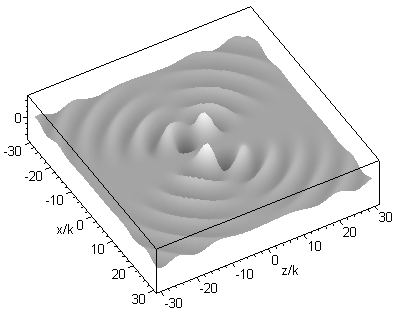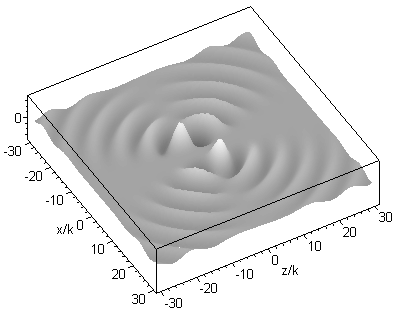
where jn are spherical Bessel functions of the first kind, k is the wavenumber, Pnm are associated Legendre functions, R = [x2 + y2 + (z - id)2]1/2, the parameter d corresponds to the Rayleigh range in the paraxial limit (i.e. d = kw02/2, with beam waist radius w0) and is the azimuth angle about the z axis. The above expression can be interpreted as a set of spherical harmonic waves centred on a complex point source-sink [Ulanowski & Ludlow 2000]. This set provides orthogonal solutions from which arbitrary beams can be constructed. The solution of order 01 corresponds in the paraxial limit to the familiar fundamental mode Gaussian beam, and in the far field it closely resembles the radiation pattern produced by a lens illuminated by a Gaussian beam. The field of the 01 order beam propagating along the z axis is shown in the graphic below for kd=2:
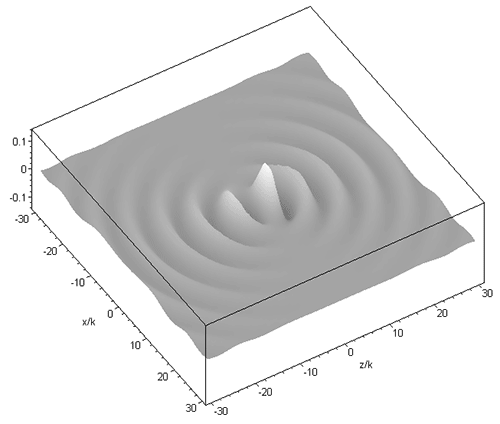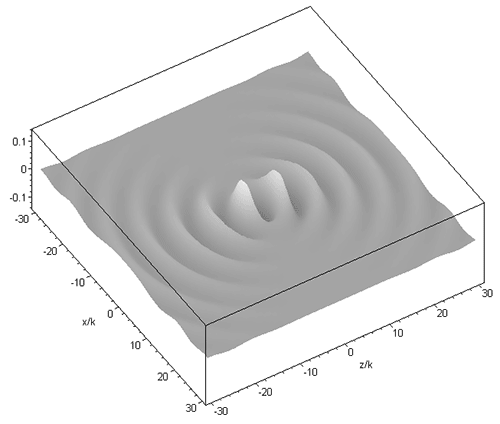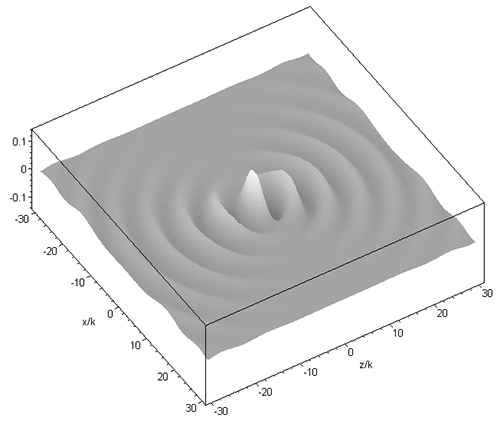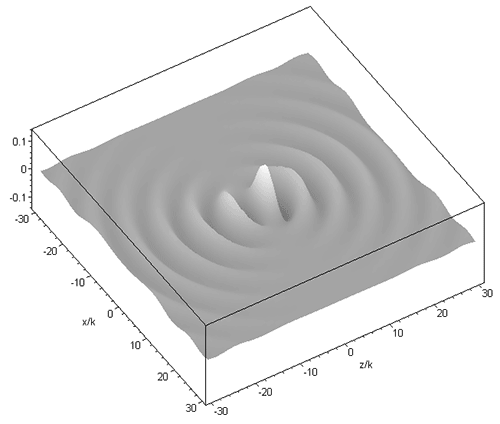
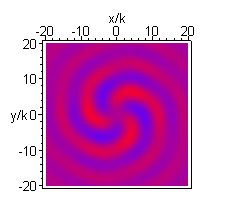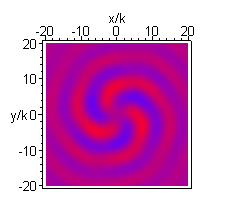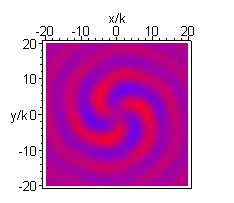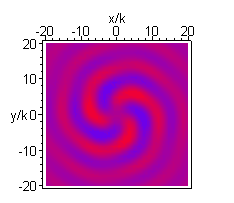
A higher order beam (m=3 n=4) is shown next, in the longitudinal (xz) and transverse (xy) plane: